공기저항을 고려한 포사체(포물선) 운동

배경지식

항력 방정식

$$ F_d = - \frac{1}{2} \rho v^2 A C_d \hat{v} $$

\( F_d \) : 항력, \( \rho \) : 유체 밀도, \( v \) : 유체에 대한 물체의 상대속도의 속력, \( A \) : 물체의 운동방향에 수직한 단면적, \( C_d \) : 항력 계수, \( \hat{v} \) : 물체의 속도방향 단위벡터

물체가 유체 내에서 움직일 때 작용하는 항력(drag force)을 계산하는 식이다. 이때 항력이란 물체가 유체 내를 움직일 때 그 움직임에 저항하는 힘이다. 수식의 마이너스 부호와 단위벡터는 항력이 물체 움직임의 반대 방향으로 작용함을 의미한다.

 

스토크스 법칙

$$ F_d = -bv $$

\( F_d \) : 항력, \( b \) : 항력계수, \( v \) : 물체의 속력

물체의 크기가 매우 작거나 속도가 매우 느린 경우, 스토크스의 법칙을 적용할 수 있다. 이에 따르면 항력은 속도에 비례한다. 수식의 마이너스 부호는 항력이 물체 움직임의 반대 방향으로 작용함을 의미한다.

---

 

가정

일반성을 잃지 않고, 지면과 평행한 방향을 x방향, 지면에 수직한 방향을 y방향으로 두자. (중력은 -y방향으로 작용하며 우리는 +x방향과 +y방향으로 물체를 발사한다고 하자.)

(0, 0)에서 질량 \( m \) 인 물체를 초기속도 \( v_0 \) 로 발사한다고 하자. 이때 초기속도의 x방향 성분을 \( v_{x0} \), y방향 성분을 \( v_{y0} \) 라 하자. 중력가속도는 \( g = 9.8m/s^2 \) 이다.

저항력이 작용하는 방향이 물체의 운동 상황에 따라 달라지므로, 우리는 x방향운동, 상승할 때의 y방향운동, 하강할 때의 y방향운동 3부분으로 나누어 계산을 진행한다.
운동 상황에 따라 힘의 방향이 달라지지만 우리는 속도를 벡터로써 다룬다. (v가 음의 값을 가질 수 있다.) 따라서 우리는 x방향운동과 y방향운동 두 부분으로 나누어 계산을 진행한다.

물체가 상승할 때의 자유도

물체가 하강할 때의 자유도

 

i) x방향

$$ F=-F_{d,x} $$

$$ \Rightarrow m \frac{dv}{dt} = -bv $$

$$ \Rightarrow \frac{dv}{v} = -\frac{b}{m} dt $$

$$ \Rightarrow \int_{v_{x0}}^{v_x} \frac{1}{v} dv = -\int_{0}^{t} \frac{b}{m} dt $$

$$ \Rightarrow \ln \frac{v_x}{v_{x0}} = -\frac{b}{m} t $$

$$ \Rightarrow v_x = v_{x0} \cdot e^{-\frac{b}{m} t} $$

$$ \Rightarrow \frac{dx}{dt} = v_{x0} \cdot e^{-\frac{b}{m} t} $$

$$ \Rightarrow \int_{0}^{x} dx = \int_{0}^{t} v_{x0} \cdot e^{-\frac{b}{m} t} dt $$

$$ \Rightarrow x = \left( - \frac{m v_{x0}}{b} \cdot e^{-\frac{b}{m} t} \right) - \left( - \frac{m v_{x0}}{b} \right) $$

$$ \therefore \ x = \frac{m v_{x0}}{b} \left( 1 - e^{-\frac{b}{m} t} \right) $$

 

ii) y방향 올라갈 때 (상승과 하강을 구분하지 않고 식을 전개한다.)

$$ F=F_g + F_{d,y1} $$

$$ \Rightarrow m \frac{dv}{dt} = -mg-bv $$

$$ \Rightarrow \frac{m}{b} \frac{dv}{dt} = -a-v \quad \left( a = \frac{mg}{b} \right) $$

$$ \Rightarrow \int_{v_{y0}}^{v_y} \frac{1}{a+v} dv = -\int_{0}^{t} \frac{b}{m} dt $$

$$ \Rightarrow \ln \left( \frac{a + v_y}{a+v_{y0}} \right) = - \frac{b}{m} t $$

$$ \Rightarrow \frac{a + v_y}{a+v_{y0}} = e^{ - \frac{b}{m} t} $$

$$ \Rightarrow v_y = -a+\left( a+v_{y0} \right) e^{ - \frac{b}{m} t} $$

$$ \Rightarrow \frac{dy}{dt} = -a+\left( a+v_{y0} \right) e^{ - \frac{b}{m} t} $$

$$ \Rightarrow \int_{0}^{y} dy = \int_{0}^{t} \left( -a+\left( a+v_{y0} \right) e^{ - \frac{b}{m} t} \right) dt $$

$$ \Rightarrow y = -at + \frac{m}{b} \left( a+v_{y0} \right) \left( 1- e^{ - \frac{b}{m} t} \right) $$

$$ \therefore \; y = -\frac{mg}{b}t + \frac{m}{b} \left( \frac{mg}{b}+v_{y0} \right) \left( 1- e^{ - \frac{b}{m} t} \right) $$

 

이 때, 포물선 운동의 최고점에서 $ v_y =0 $ 이므로, 아래 식에 대입하면

$$ v_y = -a+\left( a+v_{y0} \right) e^{ - \frac{b}{m} t} $$

$$ \Rightarrow \frac{a}{a+v_{y0}} = e^{ - \frac{b}{m} t} $$

$$ \Rightarrow t = \frac{m}{b} \, \ln \left( \frac{a+v_{y0}}{a} \right) = \frac{m}{b} \, \ln \left( 1+ \frac{b v_{y0}}{mg} \right) $$

따라서 물체가 상승하는 $ t $ 의 범위는 $ 0 \leq t \leq \frac{m}{b} \, \ln \left( 1+ \frac{b v_{y0}}{mg} \right) $

 

iii) y방향 내려갈 때  (를 추가적으로 고려해줄 필요가 없다.)

※ 초기조건: $ v_{y0'} =0 $, $ t_{0'} = \frac{m}{b} \, \ln \left( 1+ \frac{b v_{y0}}{mg} \right) $

위 조건과 ii)의 결과를 이용하여 초기위치를 구하면

$$ y_{0'} = -\frac{mg}{b} \frac{m}{b} \, \ln \left( 1+ \frac{bv_{y0}}{mg} \right) + \frac{m}{b} \left( \frac{mg}{b}+v_{y0} \right) \left( 1- \frac{\frac{mg}{b}}{\frac{mg}{b}+v_{y0}} \right) $$

$$ \Rightarrow y_{0'} = -\frac{m}{b} \frac{mg}{b} \, \ln \left( 1+ \frac{bv_{y0}}{mg} \right) + \frac{m}{b} \left( \frac{mg}{b}+v_{y0} \right) - \frac{m^2 g}{b^2} $$

$$ \therefore \; y_{0'} = \frac{m}{b} \left( v_{y0} - \frac{mg}{b} \, \ln \left( 1+ \frac{bv_{y0}}{mg} \right) \right) $$

 

$$ F=F_g + F_{d,y2} $$

$$ \Rightarrow m \frac{dv}{dt} = -mg+bv $$

$$ \Rightarrow \frac{m}{b} \frac{dv}{dt} = -a+v \quad \left( a = \frac{mg}{b} \right) $$

$$ \Rightarrow \int_{v_{y0'}}^{v_y} \frac{1}{a-v} dv = -\int_{t_{0'}}^{t} \frac{b}{m} dt $$

$$ \Rightarrow \ln \left( \frac{a - v_y}{a} \right) = \frac{b}{m} \left( t -t_{0'} \right) $$

$$ \Rightarrow v_y = a\left(1- e^{\frac{b}{m} \left(t-t_{0'}\right)} \right) $$

$$ \Rightarrow \int_{y_{0'}}^{y} dy = \int_{t_{0'}}^{t} a\left(1- e^{\frac{b}{m} \left(t-t_{0'}\right)} \right)dt $$

$$ \Rightarrow y = y_{0'} + a\left[t - \frac{m}{b} e^{\frac{b}{m} \left(t-t_{0'}\right)} \right]_{t_{0'}} ^{t} $$

$$ \Rightarrow y = y_{0'} + a \left( t-t_{0'} + \frac{m}{b} \left( 1- e^{\frac{b}{m} \left(t-t_{0'}\right)} \right) \right) $$

$$ \therefore \; y = \frac{mg}{b} \left( \frac{v_{y0}}{g} - \frac{m}{b} \ln \left( 1+\frac{bv_{y0}}{mg} \right) + \left(t-t_{0'}\right) + \frac{m}{b} \left( 1- e^{\frac{b}{m} \left(t-t_{0'}\right)} \right) \right) $$

 

이 때, $ t $ 의 범위는 $ t \geq \frac{m}{b} \, \ln \left( 1+ \frac{b v_{y0}}{mg} \right) $

 

 

iv) 그래프 그리기

그래프를 그리기 위해서 각각 x=f(t), y=g(t)의 꼴이었던 매개변수 식을 y=h(x) 꼴의 식으로 나타내어주는 것이 편하다. 그러기 위해 i)의 결과에서

$$ \ x = \frac{m v_{x0}}{b} \left( 1 - e^{-\frac{b}{m} t} \right) $$

$$ \Rightarrow 1 - e^{-\frac{b}{m} t} = \frac{bx}{mv_{x0}}$$

$$ \Rightarrow e^{-\frac{b}{m} t} = 1-\frac{bx}{mv_{x0}}$$

$$ \Rightarrow -\frac{b}{m} t = \ln \left( 1-\frac{bx}{mv_{x0}} \right) $$

$$ \therefore \ t = -\frac{m}{b} \ln \left( 1-\frac{bx}{mv_{x0}} \right) $$

 

위 결과를 각각 ii)과 iii)의 결과에 대입해주면 y=h(x)꼴의 함수로 나타낼 수 있다.

결과를 지오지브라 클래식을 이용하여 나타내면 다음과 같다. 변수에는 다음의 값을 적용했다. \( m = 0.1 \), \( b = 1 \), \( v_{x0} = 1 \), \( v_{y0} = 1 \)

틀린 이미지 입니다.

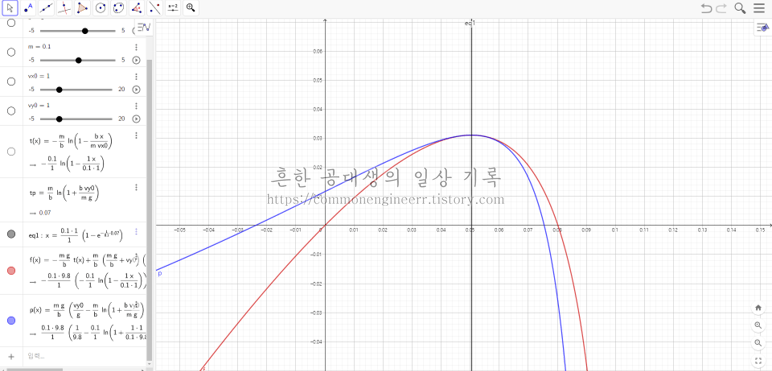
붉은 선은 y방향으로 상승할 때인 ii)의 결과를, 푸른 선은 y방향으로 하강할 때인 iii)의 결과를 나타낸다. 이때 세로 선은 최고 높이에 도달하는 지점이자, 저항력의 방향이 반대가 되는 지점이다. 이 지점 전까지는 붉은 선을 따라 상승하다가 이 지점 후부터는 푸른 선을 따라 하강한다. 상식적으로 납득할 수 있을만한 그래프를 확인할 수 있다.

 

틀린 이미지 입니다.

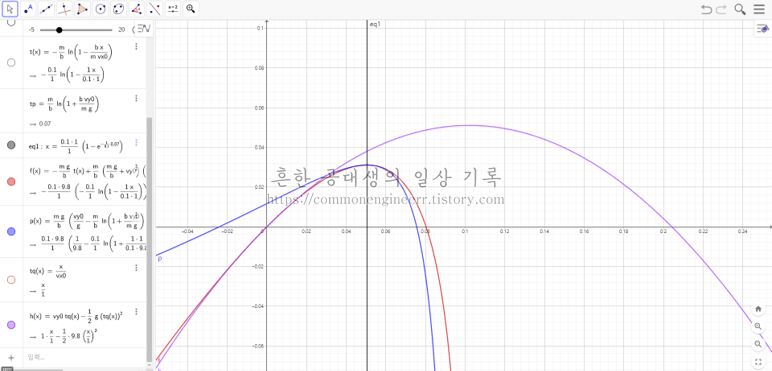
이해를 돕기 위해 공기저항이 없는 이상적인 상황(그 외의 조건은 동일)에서의 포물선운동 그래프도 함께 그려보았다. 보라색 그래프가 그것이다. 운동 초반에는 비슷한 움직임을 보이나, 결과적으로는 최고 높이나 도달 거리에서 상당한 차이가 있음을 알 수 있다.

 

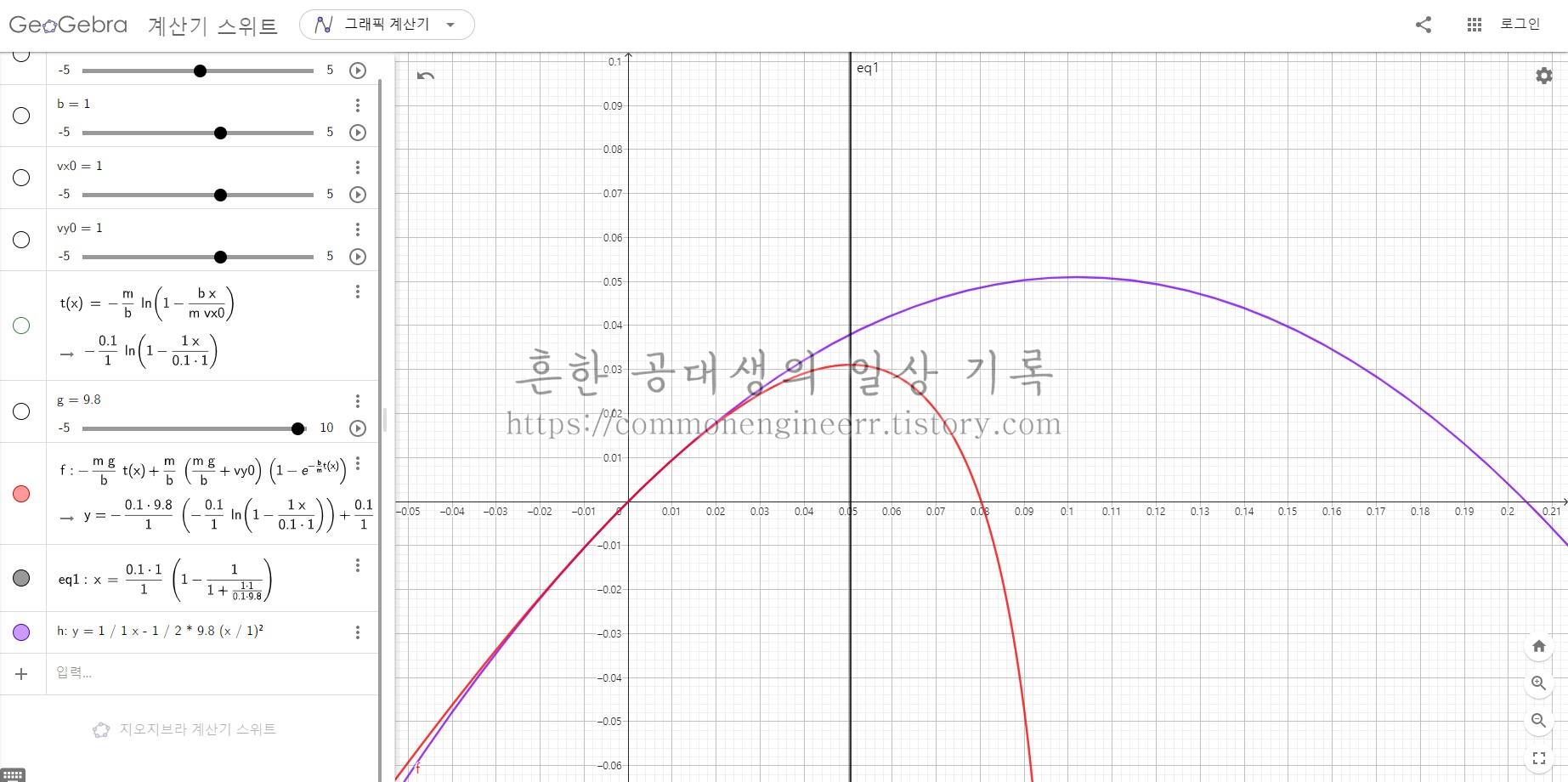
붉은 선은 우리가 계산한 결과, 즉 공기저항이 있을 때의 운동 그래프이고, 검은 선은 최고 높이에 도달한 거리를 표시했다. 보라색 선은 공기저항이 없는 경우를 나타낸 것으로, 공기저항이 포물선 운동 거리에 큰 영향을 미침을 알 수 있다.

 

추가적으로, 저항이 있는 물체는 종단속도를 가진다. 물체에 가해지는 알짜 힘이 0이 되면 속도 변화 없이 일정한 값을 가지는데, 이때의 속도를 종단속도라고 한다.

알짜힘이 0이라면,

$$ m \frac{dv}{dt} = -mg-bv_{t} = 0 $$

$$ \Rightarrow v_{t} = - \frac{mg}{b} $$

임을 도출할 수 있다.

우리가 도출한 ii)의 결과에서 시간을 무한대로 보내면,

$$ v_y = -a+\left( a+v_{y0} \right) e^{ - \frac{b}{m} t} $$

$$ \Rightarrow \lim_{t \to \infty } v_{y} = - a = - \frac{mg}{b} = v_{t} $$

이므로, 종단속도에 도달함을 알 수 있다.

 

---

수정내역

2022.11.28. iii) 하강 시에 대한 식 전개 과정에서 문제 발견. 수정조치.
2022.11.28. 종단속력에 관한 내용 추가

---